Automatic memoization of function calls in Python

The Fibonacci sequence is the integer sequence where each number is the sum of the previous two numbers, starting with zero and one:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34

Writing a function to calculate an arbitrary fibonacci number is a common problem in interviews and tests, that has an elegant if inefficient way of being solved via recursion.

Here’s a simple solution in Python:

def fib(n):
    if n < 2:
        return n
    else:
        return fib(n-1) + fib(n-2)

Given an integer n, this function will calculate the n’th number in the fibonacci sequence. If we try benchmarking this using the ever-useful timeout tool, using a value of 28:

➜ python3 -m timeit -s 'import fib' 'fib.fib(28)'
2 loops, best of 5: 109 msec per loop

Reasonably fast. But if we up this to 30…

➜ python3 -m timeit -s 'import fib' 'fib.fib(30)'
1 loop, best of 5: 291 msec per loop

A small increase almost tripled the algorithm’s runtime. If we increase this much more it will get exponentially slower to calculate, this being an O(2^n) algorithm. Why is this so inefficient?

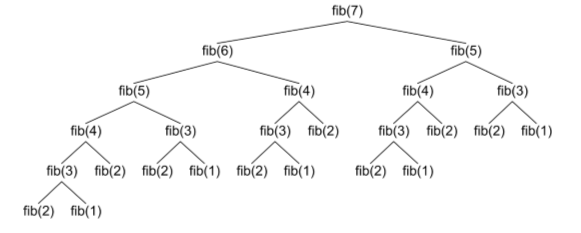
To solve this, we need to look at how the function is being called. Here’s a diagram stolen from Stack Overflow showing the recursive tree of fib(n) calls being made:

25 seperate calls altogether, with 18 of those being repeats. The percentage of repeated calls gets much worse as n increases, meaning a lot of work is being done unnecessarily.

How can we fix this, without resorting to changing our algorithm?

Introducing the LRU Cache decorator

Inside the functools standard library package, there’s a decorator called @lru_cache. This decorator records the arguments a function is called with and the value the function returned. If that function is called twice with the same arguments, the lru_cache will return the same value it got the first time, saving us the overhead of calling it twice. Since our issue is repeated function calls, we should expect a significant speedup.

Lets try timing that again after adding the decorator:

from functools import lru_cache

@lru_cache
def fib(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    else:
        return fib(n-1) + fib(n-2)

➜ python3 -m timeit -s 'import fib' 'fib.fib(30)'
2000000 loops, best of 5: 105 nsec per loop

That sped up our algorithm by about a million times. Not bad for one line of code.